MESH ANALYSIS

Introduction:
                     In Mesh analysis, we will consider the currents flowing through each mesh. Hence, Mesh analysis is also called as Mesh-current method.

                    A branch is a path that joins two nodes and it contains a circuit element. If a branch belongs to only one mesh, then the branch current will be equal to mesh current.

                    If a branch is common to two meshes, then the branch current will be equal to the sum (or difference) of two mesh currents, when they are in same (or opposite) direction.

Procedure of Mesh Analysis:
                    Follow these steps while solving any electrical network or circuit using Mesh analysis.

Step 1 − Identify the meshes and label the mesh currents in either clockwise or anti-clockwise direction.

Step 2 − Observe the amount of current that flows through each element in terms of mesh currents.

Step 3 − Write mesh equations to all meshes. Mesh equation is obtained by applying KVL first and then Ohm’s law.

Step 4 − Solve the mesh equations obtained in Step 3 in order to get the mesh currents.

                    Now, we can find the current flowing through any element and the voltage across any element that is present in the given network by using mesh currents.

Example:
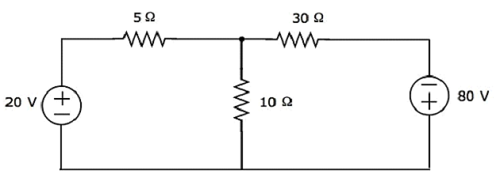
Find the voltage across 30 Ω resistor using Mesh analysis.

Step 1 − There are two meshes in the above circuit. The mesh currents I1 and I2 are considered in clockwise direction. These mesh currents are shown in the following figure.

Step 2 − The mesh current I1 flows through 20V voltage source and 5Ω resistor. Similarly, the mesh current I2 flows through 30Ω resistor and 80V voltage source. But, the difference of two mesh currents I1 and I2 flows through 10Ω resistor, since it is the common branch of two meshes.

Step 3 − In this case, we will get two mesh equations since there are two meshes in the given circuit. When we write the mesh equations, assume the mesh current of that particular mesh as greater than all other mesh currents of the circuit.

The mesh equation of first mesh is
                                            5 I1 +10(I1 - I2) = 20
                                            5I1 + 10I1 -10I2 = 20
                                                    15I1 – 10I2 = 20  
                               Divide the above equation with 5
                                                        3I1 – 2I2 = 4 -------------------- (1)

The mesh equation of second mesh is
                                            10(I2 – I1) + 30I2 = 80
                                            10I2 – 10I2 + 30I2 = 80
                                                      -10I1 + 40I2 = 80
                                Divide the above equation with 10
                                                            -I1 + 4I2 = 8 ------------------(2)

Step 4 − Finding mesh currents I1 and I2  by solving Equation 1 and Equation 2.
                                                            3I1 – 2I2 = 4 ----------------- (1)
                                                            -I1 + 4I2 = 8 ------------------(2)      
                                     
                                     (1) × 1   ⇒      3I1 – 2I2 = 4
                                     (2) × 3   ⇒  -3I1 + 12I2 = 24
                                     (1) + (2) ⇒            10I2 = 28

                                                                       I2 = 2.8A

Substitute I2 = 2.8A in Equation 2.
                                                       3I1 – 2(2.8) = 4
                                                            3I1 – 5.6 = 4
                                                            3I1 = 4 + 5.6
                                                            3I1 = 9.6

                                                              I1 = 3.2A

So, we got the mesh currents I1 = 3.2A and  I2 = 2.8A respectively.

Step 5 − The current flowing through 30Ω resistor is nothing but the mesh current   I2 and it is equal to 2.8A. Now, we can find the voltage across 30Ω resistor by using Ohm’s law.

V30Ω = I2 R
      V30Ω = 2.8 × 30
V30Ω = 84V

Therefore, the voltage across 30 Ω resistor of the given circuit is 84 V.


Comments

Post a Comment

Popular posts from this blog

Nominal 'π' method

Image
                       In the nominal pi model of a  medium transmission line,  the series impedance of the line is concentrated at the centre and half of each capacitance is placed at the centre of the line. The nominal Pi model of the line is shown in the diagram below. In this circuit, By Ohm’s law By KCL at node a, Voltage at the sending end By ohm’s law Sending-end current is found by applying KCL at node c or Equations can be written in matrix form as Also, Hence, the ABCD constants for nominal pi-circuit model of a medium line are Phasor diagram of nominal pi model The phasor diagram of a nominal pi-circuit is shown in the figure below. It is also drawn for a lagging power factor of the load. In the phasor diagram the quantities shown are as follows; OA = V r  – receiving end voltage. It is taken as reference phasor. OB = I r  – load current lagging V r  by an angle ∅ r . BE = I ab  – current in receiving-end capacitance. It leads V r  by 90°. The line current I is the phasor su
Read more

BREAKDOWN MECHANISMS IN ZENER DIODE

Image
Avalanche breakdown:                        The avalanche breakdown takes place when both sides of the junction are lightly doped and consequently the depletion region is large. When the reverse bias voltage is increased the accelerated free electrons collide with the semiconductor atoms in the depletion region. Due to the collision the covalent bonds are broken and electron - hole pairs are generated. These new charge carriers so produced acquire energy from applied potential and in turn produce additional carriers. This forms a cumulative process called as avalanche multiplication. This avalanche multiplication causes the reverse current to increase rapidly. This leads to avalanche breakdown.  Zener breakdown:                         This Zener breakdown mechanism is fundamentally different from avalanche breakdown. Zener breakdown occurs when the electric field in the depletion region increases to point where it can break covalent bonds and generate electron hole pair. The electro
Read more